
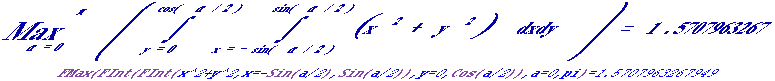
|
| Этот файл получен в результате решения 45 примеров из гида "Как вычислить" (подписи осей опущены) |
`Поставьте курсор на строку примера и выполните,
`кликнув "exe" или нажав "Enter":
(Sqrt(5)-1)/2=0.618033988749895
`Пример 2. Переменные.
`Выполните:
r=2
`площадь круга радиуса r:
s=pi*r^2
s=12.5663706143592
`объем цилиндра радиуса r высотой 3:
v=s*3
v=37.6991118430775
`Пример 3. Размерности. (В меню "Параметры" пункт
`"Учитывать размерности" должен быть помечен.)
`Относительное движение (человек в поезде):
54[км/ч]+75[м/мин]=16.25[м/с]
`Пример 4. В паспорте автомобиля американского
`производства указан расход топлива:
`30 miles per gallon.
`Сколько литров на 100 км потребляет автомобиль?
`Решение (в системе СИ объем в кубических метрах):
100[км]/30[миль/гал]=7.84048611111111E-03[м^3]
`Теперь результат можно перевести в литры:
Ans*1[м^3]/1[л]=7.84048611111111
`Пример 5. Найти падение потенциала U в медном проводе
`длиной L=500 м и диаметром d=2 мм, если ток в нем
`I=2 А.
`Решение определяется формулой: U = I·R =
`= I·r·L/(p·(d/2)^2), где r - удельное сопротивление
`проволоки, - вставляется из справочника калькулятора:
U=2[А]*1.78[мкОм·см]*500[м]/(pi*(2[мм]/2)^2)
U=5.66591597407148[В]
`Пример 6. Первая космическая скорость (Sqrt(R*g)):
Sqrt(6370[км]*9.80665[м/с^2])=7903.69283942639[м/с]
`Пример 7. При электролизе медного купороса за время
`t=1 час выделилась масса меди m=0.5 г, площадь
`каждого электрода S=75 см^2. Найти плотность тока j.
`Решение: j=m/(K·S·t), где K=(1/F)·(A/Z)
`- электрохимический эквивалент, F - число Фарадея
`A - молярная масса меди Z - валентность меди,
`вставляя данные из справочника калькулятора получим:
K=(1/96485.3383[Кл/моль])·(63.54[г/моль]/2)
K=3.2927282590043E-07[кг/(А·с)]
j=0.5[г]/(K[кг/Кл]·75[см^2]·1[ч])
j=56.2406523158349[А/м^2]
`Заметьте, для умножения всегда можно использовать
`символ "·"
`Пример 8. Запись величин с размерностями:
(1ч36'11"+23'49")[ч]=7200[с]
2[[кг]·[м]/[с]^2]=2[Н]
2[[кг·м]/[с^2]]=2[Н]
760[мм.рт.ст.]+10[м.вод.ст.]=199391.5[Па]
0[°C]=273.15[К]
0[°Ф]=255.372222222222[К]
0[°r]=273.15[К]
0[°C]+0[°C]=273.15[К]
1[°C]-1[°C]=273.15[К]
1[1/°C]=1[1/К]
1[Дж/К]=1[Дж/К]
1[Дж/°C]=1[Дж/К]
1[Дж/°Ф]=1.8[Дж/К]
1[Дж/°r]=0.8[Дж/К]
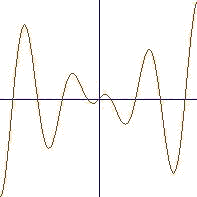
`Пример 9. Нарисовать график функции x*Cos(x):
FPlot(x*Cos(x),x=-4*pi,4*pi)
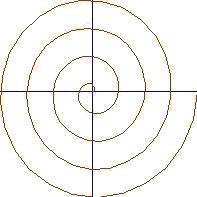
`Пример 10. Нарисовать график функции, заданной
`параметрически x(t)=t*Cos(t), y(t)=t*Sin(t):
XYPlot(t*Cos(t),t*Sin(t),t=0,8*pi)
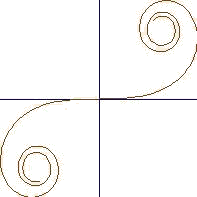
`Пример 11. Нарисовать график клотоиды (требуется
`~28000 вычислений подинтегральных функций):
XYPlot(FInt(Cos(f^2),f=0,t),FInt(Sin(f^2),f=0,t),t=-4,4,200)
`Пример 12. Решение уравнений вида f(x)=0.
`Нужно ввести функцию f(x) и интервал, в котором
`ищется корень. Если интервал заранее не известен,
`то просто используйте большой интервал.
`Решить уравнение x^3-2*x-5=0:
FZero(x^3-2*x-5,x=-3,3)=2.09455148154232
`Пример 13. Если уравнение имеет несколько корней и
`оба корня попадают в заданный интервал, то выдается
`сообщение: "Недопустимый аргумент", в этом случае,
`нарисуйте график функции и определите интервал
`визуально.
`Решить уравнение 0.6*x^2+3.2*x-8.4=0:
FPlot(0.6*x^2+3.2*x-8.4,x=-10,10)
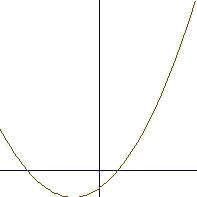
`видим, что один корень отрицательный, другой
`положительный, найдем их:
FZero(0.6*x^2+3.2*x-8.4,x=-10,0)=-7.26134958403007
FZero(0.6*x^2+3.2*x-8.4,x=0,10)=1.92801625068759
`Пример 14. найти корни уравнения x*сos(x)=0 на
`интервале -2*p<x<2*p
FPlot(x*Cos(x),x=-2*pi,2*pi)
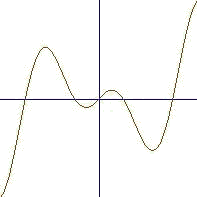
`видим, что имеется пять корней, один x=0, другие -
`симметричные относительно оси ординат:
FZero(x*Cos(x),x=0,pi)=1.5707963268199
FZero(x*Cos(x),x=pi,2*pi)=4.71238898038469
`два оставшихся корня с обратным знаком:
`x=-4.71238898038469, x=-1.5707963268199
`Пример 15. Вычислить определитель:
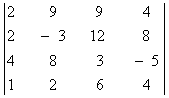
Det(2,9,9,4;2,-3,12,8;4,8,3,-5;1,2,6,4)=147
`Заметьте, в качестве разделителя параметров в любой
`функции можно использовать как "," так и ";"
`Пример 16. Решить систему линейных уравнений:
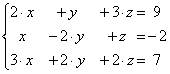
`Решение:
D=Det(2,1,3;1,-2,1;3,2,2)
D=13
Dx=Det(9,1,3;-2,-2,1;7,2,2)
Dx=-13
Dy=Det(2,9,3;1,-2,1;3,7,2)
Dy=26
Dz=Det(2,1,9;1,-2,-2;3,2,7)
Dz=39
x=Dx/D
x=-1
y=Dy/D
y=2
z=Dz/D
z=3
`Пример 17. Исследование функции f(x)=x^3-2*x-5
`объявить функцию, выполните:
f(x)=x^3-2*x-5
`нарисовать график функции:
FPlot(f(x),x=-2,3)
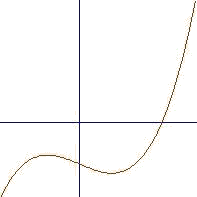
`найти корень уравнения x^3-2*x-5=0:
FZero(f(x),x=-2,3)=2.09455148154233
`найти абсциссу минимума функции:
FMin(f(x),x=-2,3)
`тогда ордината минимума:
f(Ans)=-8.88178419700125E-16
`найти абсциссу максимума функции:
FMax(f(x),x=-2,3)=-0.816496572266377
`тогда ордината максимума:
f(Ans)=-3.91133789209637
`если функция с именем "f" уже объявлена и ее
`вид отличается от x^3-2*x-5, то либо удалите эту
`функцию (пункт "Удалить функции пользователя" в
`меню "Параметры"), либо используйте другое имя
`функции, например, f0; можно также не объявляя
`функции, использовать ее выражение, сравните:
FZero(x^3-2*x-5,x=-2,3)=2.09455148154233
`Пример 18. Сумма ряда s(t)=1/2^t, t=1,2,...,100:
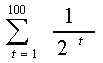
FSum(1/2^t,t=1,100)=1
`Пример 19. Интеграл от 0 до 2 функции Sin(x)/x:
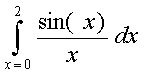
FInt(Sin(x)/x,x=0,2)=1.60541297680269
`Пример 20. Кратные интегралы. Двойной интеграл:
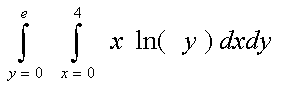
FInt(FInt(x*Ln(y),x=0,4),y=1,e)=7.99999999998562
`Пример 21. Тройной интеграл
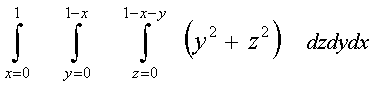
`(требуется ~37000 вычислений подинтегральной функции):
FInt(FInt(FInt(y^2+z^2,z=0,1-x-y),y=0,1-x),x=0,1)=3.33333333333333E-02
`В Ans всегда содержится ответ, выполните:
Ans=3.33333333333333E-02
`Пример 22. Решить задачу оптимизации для геометрии
`равнобедренного треугольника, - найти такой угол
`между равными сторонами равнобедренного треугольника,
`чтобы момент инерции относительно оси, проходящей
`через этот угол перпендикулярно плоскости
`треугольника, был бы максимальным
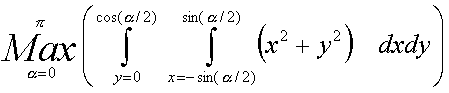
`(требуется ~8000 вычислений функции):
RadToDeg(FMax(FInt(FInt(x^2+y^2,x=-Sin(a/2),Sin(a/2)),y=0,Cos(a/2)),a=0,pi))=89°59'59.9965792301566"
`Пример 23. Циклические вычисления.
`Нарисуем в двух вложенных циклах шестнадцать эллипсов:
Do(Do(XYPlot(a*Cos(t),b*Sin(t),t=0,2*pi,-5,5,-5,5),a=1,4,4),b=1,4,4)=89.9999990497862

`Пример 24. Вычислить размер таблицы кэширования,
`не превышающий 10000 элементов памяти:
Prime(10000)=9973
`Пример 25. Способы записи десятичных чисел:
3=3
3.14=3.14
0.314E+1=3.14
0.314E1=3.14
0.314e1=3.14
31.4E-1=3.14
`Пример 26. В виде градусов минут и секунд:
23o56'4"=23.9344444444444
23o56'=23.9333333333333
56'4"=0.934444444444444
56'=0.933333333333333
4"=1.11111111111111E-03
23°=23
23°0'4"=23.0011111111111
`в этом формате функция RadToDeg(x) выводит свой результат:
RadToDeg(1)=57°17'44.8062470965669"
57°17'44.8062470965669"=57.2957795130824
`Пример 27. В виде часов минут и секунд:
23h56'4"=23.9344444444444
23H56'4"=23.9344444444444
23ч56'4"=23.9344444444444
23Ч56'4"=23.9344444444444
`Пример 28. Шестнадцатеричные числа:
#X7D4=2004
#X7D4=2004
#x7D4=2004
#H7D4=2004
#h7D4=2004
&X7D4=2004
`Пример 29. Восьмеричные числа:
#O3724=2004
#o3724=2004
&o3724=2004
`Пример 30. Двоичные:
#b11111010100=2004
#B11111010100=2004
&b11111010100=2004
`Пример 31. pi и e встроенные константы, выполните:
pi=3.14159265358979
e=2.71828182845905
`Пример 32. Операции:
`перемена знака:
-pi=-3.14159265358979
`сложение:
5+2=7
`вычитание:
5-2=3
`умножение:
5*2=10
`для умножения можно также использовать символ "·":
5·2=10
`деление:
5/2=2.5
`возведение:
e^pi=23.1406926327793
`процент:
5%=0.05
`факториалы целых чисел
`(для действительных чисел см. функцию II(x)):
5!=120
`деление нацело:
5\2=2
`остаток от деления (mod):
5:2=1
`дополнительная функция для абсолютной величины:
|-pi|=3.14159265358979
`Пример 33. Амортизация имущества за данный период.
`Оборудование стоит 2400 руб. и имеет срок службы
`10 лет. Остаточная стоимость составляет 300 руб.
`амортизация за первый день:
DDB(2400,300,3650,1)[руб.]=1.31506849315068[руб.]
`амортизация за первый месяц:
DDB(2400,300,120,1)[руб.]=40[руб.]
`амортизация за первый год:
DDB(2400,300,10,1,2)[руб.]=480[руб.]
`амортизация за второй год, используется коэффициент,
`равный 1.5 (а не метод двойного процента):
DDB(2400,300,10,2,1.5)[руб.]=306[руб.]
`амортизация за десятый год:
DDB(2400,300,10,10)[руб.]=22.1225472000002[руб.]
`график величины амортизации (с 1 по 10 год):
FPlot(DDB(2400,300,10,год),год=1,10)=22.1225472000002

`Пример 34. Будущее значение накопления
`(вклада, годового дохода, ренты):
FV(0.5%,10,-200,-500,1)[руб.]=2581.40337406013[руб.]
FV(1%,12,-1000)[руб.]=12682.503013197[руб.]
FV(11%/12,35,-2000,0,1)[руб.]=82846.2463719006[руб.]
`Предположим, предполагается вложить 1000 рублей под
`6% годовых (что составит в месяц 6%/12 или 0.5%) и
`вкладывать по 100 рублей в начале каждого следующего
`месяца в течение следующих 12 месяцев. Сколько денег
`будет на счету в конце 12 месяцев? Будущее значение
`накопления (вклада, годового дохода, ренты):
FV(0.5%,12,-100,-1000,1)[руб.]=2301.40183034091[руб.]
`Пример 35. Платежи по процентам за данный период на
`основе периодических постоянных выплат и постоянной
`процентной ставки.
`Выплаты по процентам за первый месяц для трехгодич-
`ного займа в 800000 рублей из расчета 10% годовых:
IPmt(0.1/12,1,36,800000)[руб.]=-6666.66666666667[руб.]
`Доход за последний год от трехгодичного займа в
`800000 рублей из расчета 10% годовых при ежегодных
`выплатах:
IPmt(0.1,3,3,800000)[руб.]=-29244.7129909366[руб.]
`Пример 36. Внутренняя скорость оборота (%) для ряда
`последовательных периодических операций с наличными.
`Первоначальный взнос в 70000 руб., ожидается получить
`чистый доход в течение пяти лет в следующих размерах:
`12000 руб.,15000 руб.,18000 руб.,21000 руб.,26000 руб.
`Внутренняя скорость оборота инвестиции после 4-х лет:
IRR(-70000,12000,15000,18000,21000)*100=-2.124484827347
`Внутренняя скорость оборота после пяти лет:
IRR(-70000,12000,15000,18000,21000,26000)*100=8.66309480331796
`Внутренняя скорость оборота после двух лет:
IRR(-70000,12000,15000)*100=-44.3506941334741
`Пример 37. Модифицированная внутренняя скорость
`оборота (%) средств для ряда последовательных
`периодических операций с наличными.
`Предположим, что Вы занимаетесь рыболовным промыслом
`и только что завершили пятый год работы. Пять лет
`назад Вы взяли 120000 руб. под 10% годовых для
`покупки лодки. Ваши годовые уловы принесли прибыль в
`39000 руб.,30000 руб.,21000 руб.,37000 руб. и
`46000 руб. соответственно.
`За эти годы Вы реинвестировали получаемую прибыль
`под 12% годовых.
`Тогда модифицированная внутренняя скорость оборота
`за пять лет:
MIRR(10%,12%,-120000,39000,30000,21000,37000,46000)*100=12.6094130365905
`Модифицированная внутренняя скорость оборота
`за три года:
MIRR(10%,12%,-120000,39000,30000,21000)*100=-4.80446552499807
`Модифицированная внутренняя скорость оборота за пять
`лет, если значение аргумента reinvest_rate равно 14%:
MIRR(10%,14%,-120000,39000,30000,21000,37000,46000)*100=13.4759110828315
`Пример 38. Количество периодов выплаты для данного
`вклада:
NPer(12%/12,-100,-1000,10000,1)=59.6738656742946
NPer(1%,-100,-1000,10000)=60.0821228537617
NPer(1%,-100,1000)=10.5886444594232
`Пример 39. Чистый текущий объем вклада, используя
`учетную ставку, а также объемы будущих платежей и
`поступлений.
`Рассмотрим инвестицию, при которой Вы выплачиваете
`10000 рублей через год после сегодняшнего дня и
`получаете годовые доходы 3000 руб.,4200 руб. и
`6800 руб. в последующие три года. Предположим, что
`учетная ставка составляет 10%, в таком случае чистый
`текущий объем инвестиции составит:
NPV(10%,-10000,3000,4200,6800)[руб.]=1188.44341233522[руб.]
`В предыдущем примере начальный платеж 10000 руб. был
`включен как одно из значений, поскольку выплата
`производилась в конце первого периода.
`Рассмотрим инвестиции, которые начинаются в начале
`первого периода. Допустим Вы интересуетесь покупкой
`обувного магазина. Стоимость предприятия - 40000 руб.
`и Вы ожидаете получить следующие доходы за первые 5
`лет: 8000 руб., 9200 руб., 10000 руб., 12000 руб. и
`14500 руб. Годовая учетная ставка равна 8 процентов.
`Она может представлять степень инфляции или учетную
`ставку конкурирующих инвестиций:
NPV(8%,8000,9200,10000,12000,14500)-40000[руб.]=1922.06155493237[руб.]
`В предыдущем примере начальная цена 40000 руб. не
`включалась в список значений, поскольку выплата
`пришлась на начало периода.
`Предположим, что на шестой год ваши дела шли менее
>`удачно, и ожидается убыток в 9000 руб. для шестого
`года. Чистый текущий объем инвестиции в обувной
`магазин после шести лет составит:
NPV(8%,8000,9200,10000,12000,14500,-9000)-40000[руб.]=-3749.46508701557[руб.]
`Пример 40. Выплата по ссуде на основе постоянных
`выплат и постоянной процентной ставки.
`Ежемесячные выплаты по займу в 10000 руб. и годовой
`процентной ставке 8%, которые можно выплачивать
`в течении 10 месяцев:
Pmt(8%/12,10,10000)[руб.]=-1037.03208935916[руб.]
`Для того же займа, если выплаты должны делаться
`в начале периода, то выплата составит:
Pmt(8%/12,10,10000,0,1)[руб.]=-1030.16432717798[руб.]
`Сумма, которую необходимо выплачивать Вам каждый
`месяц, если Вы дали взаймы 5000 руб. под 12% годовых
`и хотите получить назад деньги за пять месяцев:
Pmt(12%/12,5,-5000)[руб.]=1030.1989980794[руб.]
`Если требуется накопить 50000 руб. за 18 лет,
`накапливая постоянную сумму каждый месяц, можно
`определить размер откладываемых сумм. Если
`предположить, что удастся обеспечить 6% годовых на
`накопления, сколько нужно откладывать каждый месяц:
Pmt(6%/12,18*12,0,50000)[руб.]=-129.081160867995[руб.]
`При ежемесячной выплате 129.08 руб. с 6%
`накоплением в течение 18 лет, Вы получите 50000 руб
`Пример 41. Выплата на данный период на основе
`периодических постоянных платежей и постоянной
`процентной ставки.
`Значение основного платежа для первого месяца
`двухгодичного займа в 2000 руб. под 10% годовых:
PPmt(10%/12,1,24,2000)[руб.]=-75.6231860083666[руб.]
`Значение основного платежа по 10-летнему займу
`в 200000 руб. под 8% годовых:
PPmt(8%,10,10,200000)[руб.]=-27598.0534624214[руб.]
`Пример 42. Текущий объем вклада. Текущий объем -
`это общая сумма, которую составят будущие платежи.
`Предположим, что выкупается страховка, по которой
`выплачивается по 500 руб. в конце каждого месяца в
`течение 20 последующих лет. Стоимость ренты
`составляет 60000 руб. и выплачиваемые деньги
`принесут 8% годовых.
`Определить, будет ли это хорошим способом
`инвестировать капитал.
`Настоящий объем вклада составит:
PV(0.08/12,12*20,500,0,0)[руб.]=-59777.1458511878[руб.]
`Результат получается отрицательный, поскольку он
`представляет деньги, которые необходимо выплатить.
`Настоящий объем вклада (59777.15 руб.) меньше, чем
`запрашиваемая цена (60000 руб.). Следовательно,
`можно сделать вывод, что это не самый лучший способ
`инвестирования денег.
`Пример 43. Процентная ставка за один период при
`выплате ренты.
`Процентная ставка для четырехлетнего займа в
`8000 руб. с ежемесячной выплатой в 200 руб.:
Rate(48,-200,8000)*100=0.770147248821022
`Это месячная процентная ставка, так как период равен
`месяцу. Годовая процентная ставка составит:
0.77%*12=0.0924
`Пример 44. Величина непосредственной амортизации
`имущества за один период.
`Предположим Вы купили за 30000 руб. грузовик, который
`имеет срок эксплуатации 10 лет, после чего
`оценивается в 7500 руб.
`Снижение стоимости для каждого года эксплуатации
`составит:
SLN(30000,7500,10)[руб.]=2250[руб.]
`Пример 45. Годовая амортизация имущества для
`указанного периода.
`Если Вы купили грузовик за 30000 руб., который имеет
`срок эксплуатации 10 лет и остаточную стоимость
`7500 руб., то годовая амортизация за 1-й год
`составит:
SYD(30000,7500,10,1)[руб.]=4090.90909090909[руб.]
`Годовая амортизация за десятый год составит:
SYD(30000,7500,10,10)[руб.]=409.090909090909[руб.]